Em suma, os números dividem-se em grupos de acordo com suas características básicas. Assim temos os números inteiros positivos, mais presentes no nosso dia a dia (1,2,3,4…), usados para cálculos básicos. Ademais, temos também os números racionais, que são os fracionados 1/2, 2/3, 5/4 etc, e também os números irracionais, que são diferentes de todos esses.
Dessa forma, os números irracionais não podem ser resultado da divisão entre dois números inteiros, e não podem ser representados por frações irredutíveis. Então, o conjunto de números irracionais é formado pelos números decimais, que por sua vez são infinitos e não periódicos.
Dessa forma, o conjunto dos números irracionais é representado pela letra I (maiúscula). Aliás, para entender melhor, hoje iremos falar mais sobre esse conjunto de números. Vamos lá!
Origem dos números irracionais
Os números irracionais surgiram após a criação dos números racionais, que foram criados para fazer a divisão de objetos. Desse modo, quando foi criado a reta numérica, cada um dos pontos correspondiam à um único número real.
A partir disso, os matemáticos perceberam que existiam algumas brechas nessa reta numérica, e que nenhum número racional poderia corresponder a essa lacuna. Até que eles encontraram uma solução: essas lacunas deveriam ser preenchidas com números decimais infinitos e não periódicos. E assim surgiu os números irracionais.
Nessa mesma época, descobriu-se ainda que alguns desses números decimais poderiam ser raízes não exatas. Essa descoberta foi um marco muito importante, principalmente para a geometria. E isso fica muito claro quando se fala sobre o Teorema de Pitágoras, que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Vejamos um exemplo do uso do Teorema de Pitágoras a seguir:

Descoberta dos irracionais pelo Teorema de Pitágoras.
Fonte: Guia do Estudante
Nesse exemplo, a medida da diagonal de um quadrado de lado mediano 1, será √2. No entanto, o resultado dessa raiz é um número decimal infinito e não periódico, ou seja, um número irracional.
Como não é possível chegar ao valor da raiz exata, o máximo que conseguimos é um número muito próximo, mas não o valor exato.
Sendo assim, ao extrair sua raiz quadrada, obtemos o seguinte resultado:
- √2 = 1,414213562373…. (infinito e não periódico)
Outros exemplos de números irracionais:
- √3 = 1,732050807568….
- √5 = 2,236067977499…
- √7 = 2,645751311064…
Números Irracionais e Dízimas Periódicas
As dízimas periódicas, apresentam uma representação decimal infinita, contudo, não é comum considerá-las como números irracionais. Isso explica-se pelo fato de que, embora elas contenham decimais infinitos, elas ainda representam-se por meio de frações, e os números racionais não.
Portanto, as dízimas periódicas possuem sempre a mesma sequência de repetição.
Vejamos o exemplo do número 0,333…, apesar de ser decimal infinito, ele ainda pode ser escrito na forma de fração irredutível, pois:

Sendo assim, as dízimas periódicas são números racionais.
Classificação dos Números Irracionais
Além disso, os números desse conjunto classificam-se em dois tipos: algébricos e transcendentes. Vejamos cada um deles a seguir:
-
1. Números irracionais algébricos
Um número só será algébrico caso satisfaça uma equação algébrica de coeficientes inteiros.
Por exemplo:
A raiz quadrada de 2 (√2) pode ser escrita como sendo x2 – 2 = 0, então é irracional algébrico.
-
2. Números irracionais transcendentes
Já o número irracional transcendente é um número real ou complexo que não é raiz de nenhuma equação polinomial a coeficientes inteiros.
Como por exemplo:
- O número pi (π), descoberto por meio da divisão do comprimento de uma circunferência pelo diâmetro da mesma. Sendo ele o mais famoso dos números transcendentes.Π = 3,141592653589793238462…
- O número de Neper, descoberto por John Napier, representado por e, também é considerado um número irracional transcendente. Sendo aproximadamente igual a 2,718281.
- O número de ouro (divina proporção), representado por Phi (ϕ). Seu valor é ϕ = 1,618033… Encontra-se esse número através da razão áurea, seguindo a sequencia de Fibonacci.
Conjuntos numéricos
Como visto anteriormente, existem vários conjuntos números, cada um deles representado por uma letra. Assim, o conjunto dos números irracionais é representado por I, enquanto o conjunto dos números reais, é representado por R, é a união dos números racionais (Q) e números irracionais (I).
Portanto, todos os números naturais (N), inteiros (Z), racionais e irracionais são todos reais.
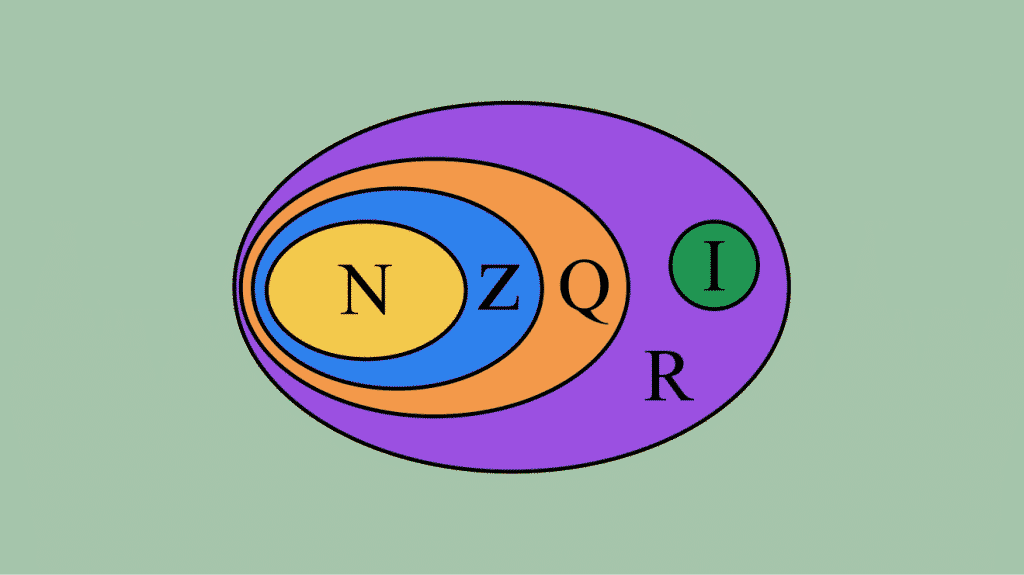
Fonte: Guia do Ensino
Enfim, o que você achou dessa matéria? E então, que tal conhecer um pouco mais sobre a vida de Pitágoras?
Fontes: Toda Matéria, Brasil Escola, Mundo Educação
Bibliografia:
- GOUVEIA, Rosimar. Números Irracionais. [20–]. Acesso em: 20 mar. 2020.
- SILVA, Luiz Paulo Moreira. “O que é o conjunto dos números irracionais?”; Brasil Escola. Acesso em: 20 mar. 2020.
- OLIVEIRA, Raul Rodrigues de. Números irracionais. [20–]. Acesso em: 20 mar. 2020.
Fonte Imagem Destacada: Revista Galilleu



