A projeção ortogonal de figuras geométricas é a sombra de um ponto sobre uma superfície plana. Nesse sentido, imagine que este ponto está sendo iluminado pelo sol exatamente ao meio dia. A silhueta formada no solo é o objeto de estudo de hoje.
Em suma, ortogonal vem do grego “Orthos”, que significa reto e “Gonia”, que quer dizer ângulo. Ao se tratar de um ângulo reto, como diz a raiz da palavra, já temos como base, portanto, o eixo do ponto. Ele é gerado através da projeção e este é perpendicular.
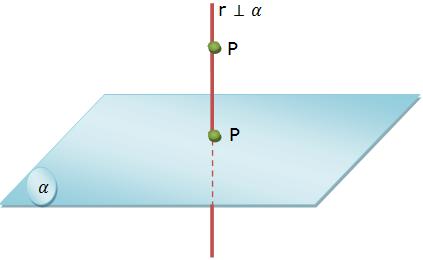
Projeção do ponto sobre o plano

Através da projeção tridimensional sobre a superfície plana bidimensional, podemos ser auxiliados no reconhecimento das características do objeto. É ai, sobretudo, que podemos executar funções simples com a ajuda da projeção da sombras.
Por exemplo, ao estacionar o carro, durante o dia, o sol refletido no veículo produz uma sombra no solo (a superfície). Essa projeção, se observarmos, nos ajuda a estacionar, porque se sua sombra estiver desalinhada, algo está errado com o alinhamento do carro na vaga.
Por fim, quando é um ponto é colocado perpendicular em uma superfície plana e, acima desse ponto, uma luz, o resultado disso é a formação de uma sombra como exemplificado acima.
Variações da Projeção Ortogonal
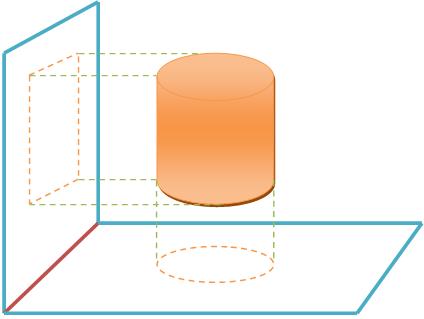
Mas, preste bem atenção no que é projetado. Se você não souber o que é o seu objeto o perigo de enganar é muito grande, pois nem tudo que parece é. Quando mudamos o ângulo da luz, a projeção muda e, junto a ela, a figura também se modifica. Veja na situação a seguir.
O cilindro, por sua vez, está localizado a um ponto x da superfície ele é o objeto que será projetado. Dessa forma, é lançado sobre ele, pela direita, um ponto de luz que cria na parede uma figura, ou uma sombra do objeto.
Como pode-se ver, o formado que surgiu na parede do lado esquerdo é quadrado, ou seja, totalmente o contrário do que seria o objeto real. Mas, na verdade, o objeto original é um cilindro.
Do mesmo modo, isso pode acontecer quando a luz está a cima do cilindro. Neste caso, veremos na superfície uma projeção em círculo. Se estivermos por baixo, afinal, acreditaremos fielmente nisso, pois a nossa visão será realmente um círculo. Contudo, a realidade é que com uma leve inclinação da luz, descobriremos que se trata de um cilindro.
Dê uma olha na tirinha abaixo e perceba o quanto o ponto de vista é importante na projeção ortogonal.
Exemplo 2
Vejamos, portanto, em uma outra situação de projeção ortogonal que pode acabar nos confundindo a realidade. Se pegarmos uma moeda que tem o formato de um círculo e colocarmos em ponto perpendicular a superfície plana teremos uma sombra de círculo.
Mas, caso a moeda estando no mesmo ponto, porém em pé, seja projetada perpendicularmente sobre a superfície plana, ao contrário de um círculo teremos a projeção de uma reta.

Ângulo na projeção ortogonal
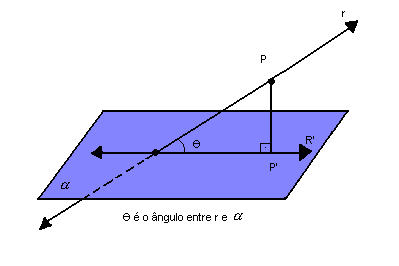
Antes de falarmos sobre ângulo retomemos, então, ao conceito de reta perpendicular. Este termo de refere, sobretudo, a uma posição que está exatamente a 90º. O ângulo formado entre a projeção e a superfície, através um ponto perpendicular, é chamado de reta.
Dependendo, enfim, da posição do objeto projetado, o ângulo gerado ente o eixo da figura tridimensional e a superfície pode mudar. Neste segundo caso, por fim, o declive gerado é decorrente da posição do objeto e da sua iluminação. Ou seja, não corresponde a eixo de 90º.
Por fim, leia também sobre Circunferência – O que é, características e geometria analítica