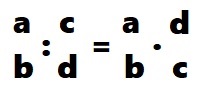As operações com frações são recorrentes na matemática e tem variações fáceis de aprender. A fração é a representação da parte de um todo. Imagine uma pizza como o todo, e suas fatias como as frações, as partes, divididas de forma igual.
Ante de tudo, nas operações com frações, há a possibilidade de somar, subtrair, dividir e multiplicar. Para realizar, enfim, o cálculo, temos dois importantes números presentes na estrutura: o valor em cima é chamado de numerador e o debaixo denominador.
Adição de frações

Primeiramente, as somas entre frações necessitam, de princípio, identificar se os denominadores, número 3 no exemplo acima, são iguais. Caso forem diferentes um outro processo se acrescenta na operação.
Denominadores iguais

É bem simples, conserva-se, sobretudo, os denominadores iguais e efetua, então, a soma dos numeradores.
Exemplo: 6/10 – 3/10 = 3/10, ou 4/6 + 3/6 = 7/6
Mínimo Múltiplo Comum
Antes de prosseguir, vamos relembrar o que é o Mínimo Múltiplo Comum, ou MMC, porque precisaremos dele para fazer o operação entre frações de denominadores diferentes. Essa regrinha básica da aritmética nada mais é que o valor menor em comum entre dois, ou mais números.
Dessa forma, teremos números inteiros e positivos como nesse exemplo: M (2) = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …} e M (8) = {8, 16, 24, 32, 40, 48, 56, 64, 72, 80, …}. Aqui podemos ver que entre os múltiplos de 2 e 8 o número 8 e 16 são comuns entre si. Eles, portanto, são os múltiplos comuns.
Denominadores diferentes
Aprendido o MMC, os denominadores diferentes vão precisar dessa identificação, vejo no exemplo:
Exemplo: 2/3 + 5/6 = 4/6 + 5/6 = 9/6
Vamos, então, entender o que aconteceu acima. Para igualar os denominadores, encontramos o seu MMC 6, que é dividido pelos denominadores originais em ambas as frações. Veja, portanto, que os denominadores se igualaram e somamos os numeradores como no caso anterior.
Subtração de frações
Em síntese, a subtração entre frações ocorre da mesma forma que ensinamos anteriormente. O exemplo a seguir mostra o quão fácil é: 7/15 – 3/9 = 21/ 45 – 15/45 = 6/45.
Observação: o MMC é necessário, sobretudo, nas operações de adição e subtração. Caso contrário, portanto, não será necessário realizar esse processo.
Multiplicação de operações com frações

Da mesma forma que anteriormente, a operação ocorrerá entre numerador com numerador e denominador com denominador, porém, dessa vez, multiplicando. Veja:
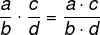
Exemplo:
2/5 . 2/2 = 4/10
Divisão de frações

A divisão, portanto, é a mais peculiar dos casos na fração. Para realizar a continha é necessário que conserve a primeira fração e multiplique pelo inverso da segunda fração. Observe o exemplo abaixo:
Como pode ver, a primeira fração a/c se manteve e a c/d foi invertida para d/c. Feito isso basta multiplicar numerador com numerador e denominador com denominador, como já havíamos visto.
Por exemplo:
Por fim, leia também sobre Circunferência – O que é, características e geometria analítica
Fonte: Escola kids, Brasil escola, Maxi educa. Educa Mais Brasil, Toda Matéria, Matemática do Aluno.
Imagem de destaque: Youtube