Diagrama de Venn, o que é? Definição, características e aplicações

Os conjuntos numéricos são parte importante no estudo da álgebra, onde funções e inequações podem ser resolvidas de maneira mais simplificada. Sendo assim, os elementos, propriedades e todos os problemas que envolvem os conjuntos são representados graficamente pelo diagrama de Venn.

Basicamente, os conjuntos dentro desta representação gráfica é formada por circunferências que se cruzam e formam subconjuntos. Após a formação dos círculos, bem como de suas intersecções, os elementos dos conjuntos são inseridos. Além disso, quando a intenção é representar o universo, os círculos são postos dentro de um retângulo, por exemplo.

A principal intenção em utilizar o diagrama de Venn é tornar as operações básicas de conjuntos mais fáceis. Dentre as operações que envolvem os conjuntos, temos a relação inclusão e pertinência, união e intersecção, diferença e conjunto complementar.

Diagrama de Venn

O diagrama de Venn, assim como o nome sugere, é um diagrama feito em homenagem ao matemático John Venn, que também desenvolvia trabalhos como filósofo. Basicamente, a versão deste diagrama é uma atualização de outros sistemas que já haviam sido desenvolvidos por matemáticos, como Leibniz, George Boole e Augustus De Morgan.

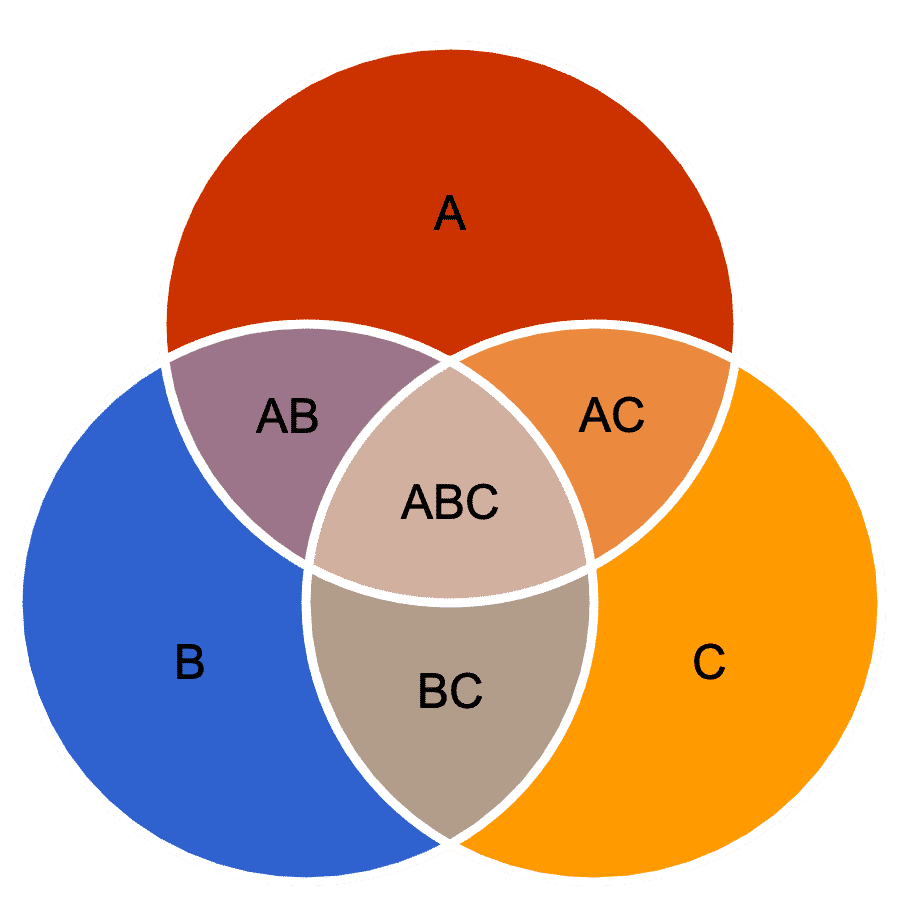
Além da matemática e da lógica, onde o diagrama serve para facilitar as equações envolvendo conjuntos, o diagrama de Venn também é útil em outras áreas do conhecimento. Portanto, pode ser utilizado, por exemplo, na ciência da computação, na logística, em pesquisas de mercado, etc.

Sendo assim, o diagrama é formado por uma linha fechada, onde os elementos de um conjunto são postos. Além disso, as linhas não se entrelaçam, sendo possível a representação de um ou vários conjuntos de forma simultânea.

Dessa forma, temos algumas denominações específicas, como a inclusão entre conjuntos, a intersecção entre conjuntos, a união entre conjuntos, diferença entre conjuntos e a forma complementar.

Inclusão entre conjuntos

Quando elementos de um conjunto fazem parte de outro conjunto, temos uma inclusão entre conjuntos. Neste caso, suponhamos que existam o conjunto A e B. Portanto, uma inclusão entre os conjuntos ocorre quando elementos do conjunto A fazem parte do conjunto B.

Dessa forma, no diagrama de Venn, dizemos que A está contido em B, ou seja, A ⊂ B. Então, esta é a representação gráfica de uma inclusão entre conjuntos, que também pode ser lida da seguinte forma: B ⊃ A, ou seja, B contém A.

Intersecção entre conjuntos

Já a intersecção entre conjuntos ocorre quando elementos de conjuntos diferentes possuem partes em comum. Ou seja, existem elementos que fazem parte de A, mas que também contemplam o conjunto B.

Neste caso, a representação gráfica é formada por A ⋂ B, onde lê-se A intersecção B. Para exemplificar melhor, imagine dois conjuntos que são postos juntos apenas pela parte do meio. Logo, este meio é a parte gráfica do conjunto, que forma então a intersecção.

Um exemplo de intersecção é: 

A = { 1, 3, 5, 7, 9, 11} 

B= {8, 9, 10, 11, 12}

A ⋂ B = {9, 11}

Diagrama de Venn – união entre conjuntos

O diagrama de Venn define que a união entre conjuntos ocorre quando os elementos do conjunto A e B se unem, ou seja, são somados entre si. Para representar esta formação, utilizamos A ⋃ B. Suponhamos que exista o conjunto A com {3, 4, 5, 6} e o conjunto B com {0, 1, 2, 3, 4, 5, 6}. Sendo assim, temos:

A = {3, 4, 5, 6} 

B = {0, 1, 2, 3}

 A ⋃ B = {0, 1, 2, 3, 4, 5, 6} 

Diferença entre conjuntos

Neste caso, são conjuntos onde os elementos que não fazem parte de ambos os conjuntos, tipo A e B, são eliminados. Nesse sentido, os elementos que não pertencem A e que, também, não fazem parte do conjunto B, são eliminados da operação. A diferença, portanto, é representada da seguinte forma: A – B. Por exemplo:

A = { 1, 2, 3, 4}

B = {1, 4, 6}

A – B= {2, 3}

B – A = {6}

Complementar

Na teoria dos conjuntos, a forma complementar é sempre aquela determinada pelos elementos que não fazem parte do conjunto A, mas que estão contidos no conjunto Universo U. Sendo assim, são todos os elementos que não estão no conjunto A, mas fazem parte do diagrama de Venn. 

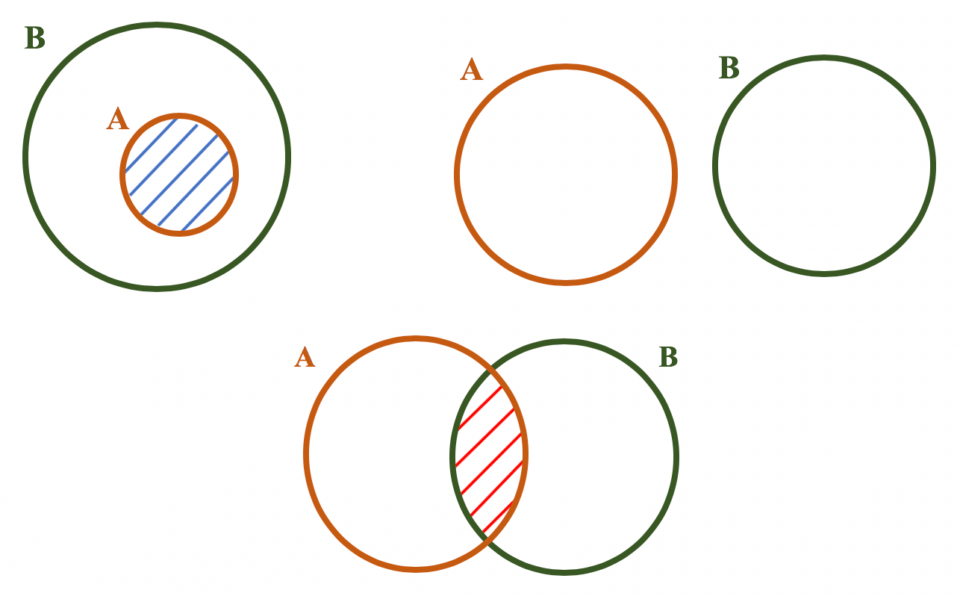
Neste caso, a representação gráfica da forma complementar é formada por: {x ∈ U | x ∉ A}. Isso significa que todo x pertence a U, ou seja, ao Universo, mas x não pode pertencer ao conjunto A. Um exemplo para esta aplicação é:

Conjunto A = {0, 1, 2}

Conjunto B = {0, 1, 2, 5, 6} 

B ⊂ A = B – A

B ⊂ A = {0, 1, 2}