Dentro das ciências exatas, os vetores são segmentos de retas orientados. Desse modo, apresentam módulo, direção e sentido, indicando grandezas físicas vetoriais. Ou seja, só podemos expressá-las ao saber seu valor numérico, se atuam na horizontal, vertical ou diagonal, bem como se vão para cima ou para baixo, para a esquerda ou para a direita.
Os vetores são representados por setas e, para desenhá-los é preciso levar em conta o seu tamanho. Por exemplo: uma grandeza de valor numérico 8 deve ser desenhada com o dobro do tamanho de uma que valor 4.
Já para definir as direções, usa-se um sistema de coordenadas. Um bastante comum é o sistema cartesiano, por exemplo. Nele as direções do seriam x e y são, respectivamente, as componentes horizontal e vertical.
Portanto, um vetor poderia ser escrito como V = (x, y). Desse mesmo modo, o sentido está relacionado à ponta do vetor, indicando se é positivo ou negativo.
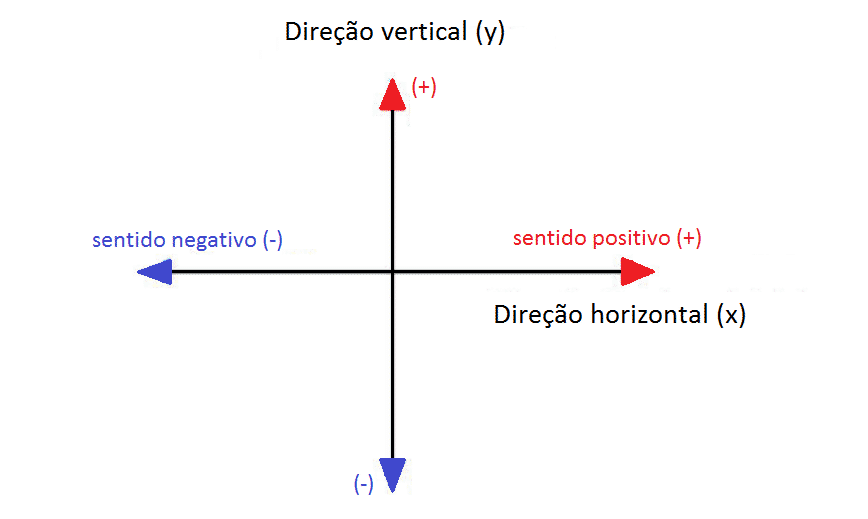
Existe também a possibilidade de um vetor estar inclinado. Logo, não coincide com nenhuma das coordenadas. Entretanto é possível calcular o tamanho de suas componentes a partir do ângulo θ. Este se forma entre o vetor e a direção horizontal, e o módulo do vetor a.

Então, para calcular as componentes nós usamos:
ax= a.cos θ (lê-se ax é igual a a multiplicado pelo cosseno do ângulo θ)
ay= a.sen θ (lê-se ay é igual a a vezes o seno do ângulo θ)
Após descobrir o valor das componentes ax e ay de um vetor, calcula-se o módulo a partir do teorema de Pitágoras: |a| = √ ax² + ay2 (módulo a é igual a raiz quadrada de ax² mais ay2)
Grandezas
Uma grandeza é aquilo que pode ser medido. Através dos vetores, podemos calcular dois tipos de grandezas:
- Escalares: é definida apenas a partir do seu módulo. Isto é, um valor numérico seguido de uma unidade de medida. Alguns exemplos são massa (gramas), temperatura (graus) e energia (joule). Sendo assim, ao dizer que a temperatura média é de 25 °C, não é necessário um complemento.
- Vetoriais: para calcular é preciso do valor numérico, direção e sentido. Podemos citar aqui força (Newton), velocidade (metro por segundo) e aceleração (velocidade por tempo). Dessa forma, ao dizer que uma força de 150 N se aplicou, também é importante compreender se foi na horizontal, vertical ou diagonal, e se veio da direita, esquerda, de cima ou debaixo.
Operações com vetores
As operações vetoriais são diferentes das operações algébricas. Só é possível somar ou subtrair os módulos dos vetores se suas direções forem iguais. Entretanto, se as direções forem diferentes é necessário usar outras regras para determinar o vetor resultante.
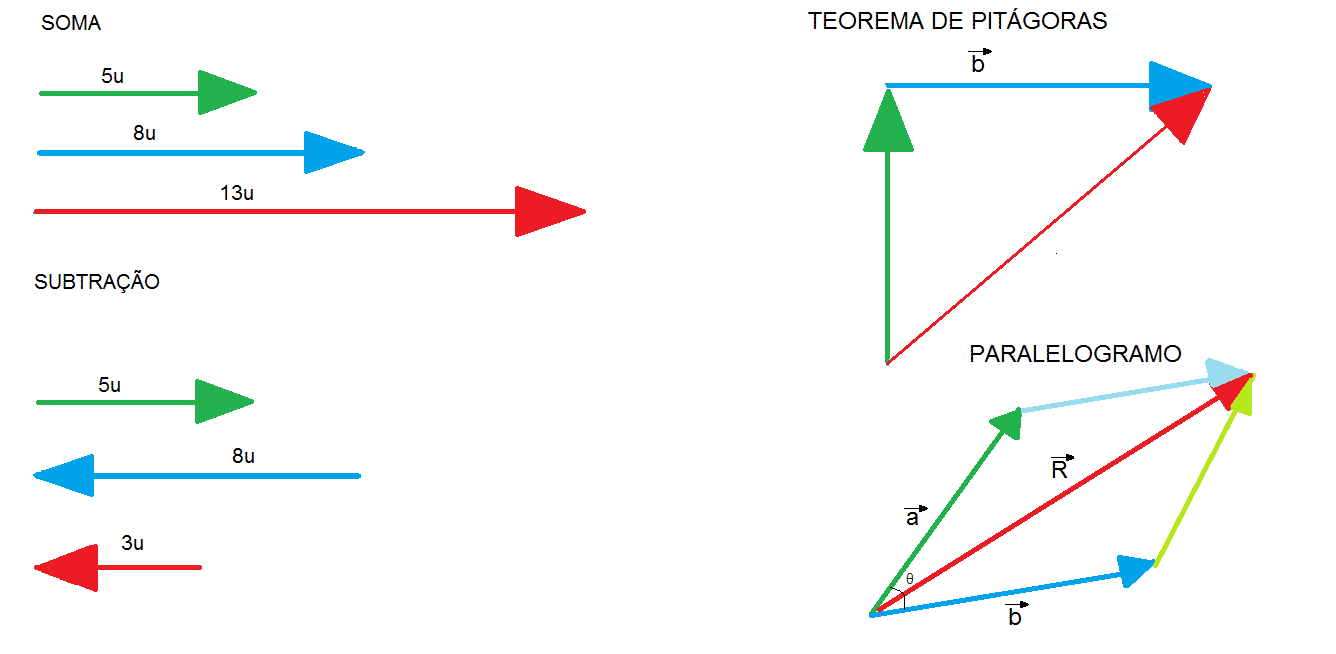
- Soma: basta somar os módulos. O resultante terá o tamanho, direção e sentido dos dois vetores originários. Então, usamos: |R̅|= |a̅ + b̅|
- Subtração: a direção dos vetores é a mesma, mas seus sentidos são opostos. O módulo do resultante é dado pela diferença entre os originários. Contudo, sua direção e sentido serão determinados pelo vetor maior. Usamos:|R̅|= |a̅ – b̅|
- Teorema de Pitágoras: vetores perpendiculares formam um ângulo de 90º. Então, ligamos o início de um vetor ao final do outro. Dessa forma, obtemos a hipotenusa. Para calcular o resultante: |R̅|² = |a̅|² + |b̅|²
- Vetores oblíquos: nesses casos é necessário o uso da regra do paralelogramo. É formado um ângulo θ entre dois vetores, e o módulo do vetor resultante é formado ela expressão: |R̅|² = |a̅|² + |b̅|² = 2|a|.|b|.cosθ
Conseguiu entender esse conteúdo de matemática? Então, aproveita para ver outros textos como Trigonometria, o que foi, origem e conceitos básicos.
Fontes: Brasil Escola e Mundo Educação.
Imagem de destaque: Pxhere.



