Conhecidos como Números Reais, o conjunto de elementos representado pela letra R engloba os conjuntos de números Naturais, conhecido pela letra N; Inteiros, representado pela letra Z; Racionais, definidos pela letra Q; e, por fim, os Irracionais , cujo símbolo é a letra I.
Os números reais são, pois, o conjunto numérico mais conhecido e utilizado, tendo em vista que qualquer número (sendo ele inteiro ou decimal) pertence a esse conjunto.
São, assim, a junção entre os conjuntos numéricos racional e irracional.
Conjunto dos Números Reais

Assim, a junção dos conjuntos, que define os números reais, é representada, portanto, com as seguintes expressões:
R = N U Z U Q U I
na qual:
R: Números Reais;
N: Números Naturais;
U: União;
Z: Números Inteiros;
Q: Números Racionais.
e, por fim, os
I: Números Irracionais
Lê-se a expressão, portanto, da seguinte forma: Conjunto dos reais = (conjunto dos naturais) união (conjunto dos inteiros) união (conjunto dos racionais) união (conjunto dos irracionais).
ou R = Q U I
onde:
R: Números Reais
Q: Números Racionais
U: União
e, por fim:
I: Números Irracionais
Desse modo, lê-se a expressão da seguinte forma: Conjunto dos reais = (conjunto dos racionais) união (conjunto dos irracionais).
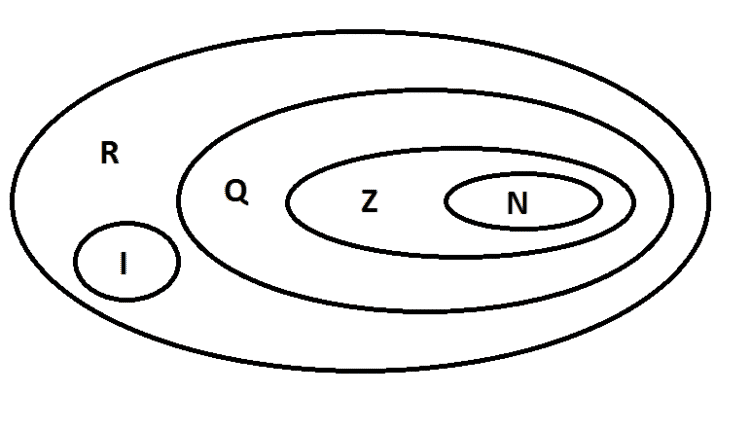
Assim, a observação do diagrama acima leva, consequentemente, às seguintes considerações:
- O conjunto dos números reais (R) reúne, portanto, os quatro conjuntos de números a seguir: Naturais (N), Inteiros (Z), Racionais (Q) e Irracionais (I);
- O conjunto dos números Racionais (Q) é, desse modo, constituído pelos seguintes conjuntos: Números Naturais (N) e Números Inteiros (Z). Assim, consequentemente, todo Número Inteiro (Z) é Racional (Q), ou em outras palavras: Z está contido em Q;
- O Conjunto dos Números Inteiros (Z) engloba, por fim, os Números Naturais (N), ou seja, todo número natural é também um número inteiro: N está contido em Z.
Os termos numéricos

Dessa forma, de modo a melhor compreender o exposto até então, estudemos, pois, os conjuntos numéricos que formam os números reais. São eles:
Conjunto dos números naturais: formado apenas por números iguais ou maiores do que zero.
N = {0, 1, 2, 3, 4, 5,…}
Conjunto dos números inteiros: números inteiros positivos ou negativos.
Z= {…, -3, -2, -1, 0, 1, 2, 3,…}
Conjunto dos números racionais: todo número que pode ser expresso em uma fração de dois números inteiros.
Q = {…,1/2, 3/4, –5/4…}
Conjunto dos números irracionais: não podem ser expressos em fração. São, dessa forma, números que apresentam infinitas casas decimais, ou seja, são uma dízima periódica.
I = {…,√2, √3,√7, 3,141592….}
Gostou desse artigo? Então, leia também sobre Progressões Aritméticas e Operações com conjuntos.
Fontes: InfoEscola, Toda Matéria, Brasil Escola.
Imagens: Escola Educação, Professor Ferretto, Revista Galileu, Passei Direto.



