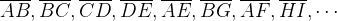Os poliedros são figuras tridimensionais. Elas são formadas por meio da união de polígonos regulares, na qual os ângulos poliédricos são todos congruentes.
Dessa forma, a união dos polígonos forma elementos que fazem parte da composição do poliedro: as vértices, arestas e faces. Em resumo, o nome poliedro vem do latim poli = muitos e edro = face.
Ou seja, são figuras com muitas faces, isto é, figuras tridimensionais onde é possível observar não apenas a largura e o comprimento, mas também a profundidade.
Sendo assim, os poliedros são classificados em pirâmides ou prismas, que são variações da mesma definição.
Contudo, vale notar que nem todas as figuras tridimensionais são poliedros, um exemplo disso são as figuras com faces curvas conhecidas como corpos redondos.
Portanto, os poliedros são as pirâmides, os prismas e os sólidos de Platão. Por outro lado, os não poliedros são conhecidos como corpos redondos ou sólidos de revolução. Por exemplo, o cone, o cilindro e a esfera.
Em síntese, a fórmula matemática que relaciona os elementos de um poliedro é chamada de Euler. Sendo que os poliedros se dividem em dois grupos: os poliedros convexos e os não convexos.
Além disso, existem alguns poliedros que exigem uma atenção especial. Eles são chamados de poliedros de Platão: tetraedro, hexaedro, octaedro, dodecaedro e, por fim, icosaedro.
Poliedros convexos
Os poliedros podem ser de dois tipos: convexos e não convexos. Primeiramente, um poliedro é convexo quando ele é formado por polígonos convexos. Sendo assim, as seguintes condições devem ser aceitas:
-
Dois dos polígonos nunca são coplanares. Ou seja, não pertencem ao mesmo plano.
-
O plano que contém qualquer um desses polígonos deixa os demais polígonos no mesmo semiespaço.
-
Cada lado de um desses polígonos pertence a apenas dois polígonos.
Elementos de um poliedro convexo
Vamos levar em conta o seguinte poliedro convexo:

Nele temos:
1- Faces
Na figura, os quadriláteros são as faces do poliedro. Neste caso são: ABGF, AEJF, EJID, DIHC e BCGH.
2- Pentágonos
As faces e a base do poliedro são chamadas de base pentagonal. Portanto, são eles: ABCDE e FGHIJ.
3- Arestas
As arestas são os segmentos que formam cada uma das faces do poliedro. Sendo assim, temos:
4- Vértices
Por fim, os pontos onde as arestas se encontram são as vértices. São elas: A, B, C, D, E, F, G, H, I, J.
5- Segmento de reta
O segmento de reta JC é denominado diagonal do poliedro, denotada por: 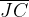
JC é uma das diagonais. Sendo que a diagonal do poliedro é o segmento de reta que une dois vértices não pertencentes à mesma face.
Além disso, temos o ângulo poliédrico, formado entre as arestas, denotado por: BÂE.
Vale destacar que um ângulo poliédrico é chamado de triédrico quando as três arestas se originam em um vértice. Além disso, é chamado de tetraédrico, se as quatro arestas tiverem origem em um vértice, e por aí vai.
Portanto, temos algumas notações:
-
Faces – F
-
Arestas – A
-
Vértices – V
Propriedades de um poliedro convexo
Algumas propriedades de um poliedro convexo são:
Propriedade 1
A soma das arestas de todas as faces equivale ao dobro do número de arestas do poliedro. Por exemplo, imagine que você quer determinar a quantidade de arestas de um poliedro com 6 faces quadradas.
Segundo a propriedade 1, basta multiplicar o número de arestas de uma face pela quantidade de faces. Sendo que isso equivale ao dobro do número de arestas. Portanto, temos:
2 . A = 4 . 6
A = 24 / 2
A = 12 arestas
Propriedade 2
A propriedade 2 diz que: a soma dos vértices de todas as faces equivale à soma das arestas de todas as faces, que é igual ao dobro do número de arestas.
Vamos supor que você deseja determinar a quantidade de arestas de um poliedro com 5 ângulos tetraédricos e 4 ângulos hexaédricos.
Como você já sabe, a soma das arestas de todas as faces é igual ao dobro do número de arestas. Sendo que o número de arestas é dado pelo produto de 5 por 4 e 4 por 6, pois são 5 ângulos tetraédricos e 4 hexaédricos. Dessa forma:
2 . A = 5 . 4 + 4 . 6
A = 44 / 2
A = 22 arestas
Poliedros côncavos ou não convexos
Em síntese, um poliedro é não convexo, ou côncavo, quando tomamos dois pontos em faces distintas e a reta r que tem esses pontos não fica toda contida no poliedro.
Um exemplo disso é a imagem abaixo:

Observe que a reta (em azul) não está completa no poliedro. Portanto, o poliedro (em rosa) é côncavo ou não convexo.
Poliedros regulares
Em resumo, um poliedro é regular quando suas faces são polígonos regulares iguais entre si e com os ângulos poliédricos todos iguais. Um exemplo disso é o cubo, pois ele conta com 6 faces, 8 vértices e 12 arestas.

Dessa forma, todas as suas faces são polígonos regulares. Sendo que as suas faces são formadas por quadrados e as arestas são todas congruentes, ou seja, têm a mesma medida.
Relação de Euler e quais são eles
A relação de Euler ou teorema de Euler, foi um resultado aprovado por Leonhard Euler (1707 – 1783).
Em resumo, ele garante que em todo poliedro convexo fechado é válida a seguinte relação: V + F = A + 2
Dessa forma, é conhecido como poliedro de Platão todos os que se enquadram nos seguintes critérios:
-
É válida a relação de Euler
-
Todas as faces apresentam o mesmo número de arestas
-
Por fim, todos os ângulos poliédricos possuem o mesmo número de arestas
Enfim, existem apenas cinco poliedros regulares e convexos, são eles:
1- Tetraedro regular

Primeiramente, o tetraedro tem 4 faces triangulares congruentes e 4 ângulos triédricos congruentes.
2- Hexaedro regular

Já o hexaedro regular conta com 6 faces quadrangulares congruentes e 8 ângulos triédricos congruentes.
3- Octaedro regular

Em contrapartida, o octaedro tem 8 faces triangulares congruentes e 6 ângulos tetraédricos congruentes.
4- Dodecaedro regular

Enquanto isso, o dodecaedro regular tem 12 faces pentagonais congruentes e 20 ângulos triédricos congruentes.
5- Icosaedro regular

Por fim, o icosaedro regular conta com 20 faces triangulares congruentes e 12 ângulos pentaédricos congruentes.
Você sabia?
-
Platão, ao estudar os poliedros regulares, listou cada um com elementos referentes à natureza. Como resultado disso, as figuras platônicas denominam-se também, sólidos platônicos;
-
Pois bem, em seu tratado filosófico intitulado Timeu, Platão apresenta terra, ar, água e fogo como cubo, octaedro, icosaedro e tetraedro , respectivamente. Por sua vez, o dodecaedro representa o universo;
-
Por fim, o Teorema de Euler foi descoberto em 1758, entretanto, em 1639, o filósofo René Descartes produziu um manuscrito no qual apresentou a mesma fórmula de Euler.
Fontes: Brasil Escola, Brasil Escola, Matemática Básica, e, por fim, Toda Matéria.
Bibliografia:
- LUIZ, Robson. “Poliedros”; Brasil Escola.
- LIMA, Elon Lages. O TEOREMA DE EULER SOBRE POLIEDROS. Revista Matemática Universitária, [S.L], n. 2, p. 57-74, dez. 1985. Semestral.
- PEREIRA, Hamilton Soares. Poliedros platônicos. 2011. 42 f. Monografia (Especialização) – Curso de Matemática, Universidade Federal de Minas Gerais, Belo Horizonte, 2011.