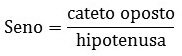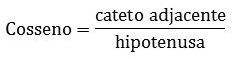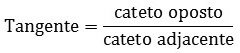A Trigonometria é uma parte da Matemática encarregada de estudar as relações ocorridas entre os lados e os ângulos dos triângulos.
Ela é usada atualmente em diferentes áreas de estudo, desde teoria musical a navegação de satélite. Mas também pode ser empregada, por exemplo, na química, biologia, geografia e até na medicina.
Seu emprego vem da época da Babilônia, embora os gregos sejam mais famosos no seu emprego. O Pai da Trigonometria é o grego Hiparco de Niceia, posto que a introduziu nos estudos científicos.
Contexto Histórico
A palavra “trigonometria” vem do grego e corresponde às palavras trigono (triângulo) e metrein (medidas). Mas há uma teoria de que os primeiros a usá-la foram os babilônicos e não os gregos.
A história da Trigonometria provavelmente vem da necessidade dos astrônomos de precisar seus cálculos. Mas foi amplamente utilizada no aperfeiçoamento das técnicas antigas de navegação.
A introdução da Trigonometria nos estudos científicos, no entanto, se deve ao astrônomo grego Hiparco de Niceia, que viveu entre os anos 190 a.C. e 120 a.C.. Essa é a razão de ser ele lembrado como o Pai da Trigonometria.
O que são as funções trigonométricas
As funções trigonométricas podem ser definidas como aquelas que dizem respeito aos triângulos retângulos, ou seja, que têm um ângulo de 90°. Elas são: seno, cosseno e tangente.
As funções trigonométricas estão nas razões que existem entre dois lados do triângulo em função dum ângulo. Ela são constituídas por dois catetos, que são oposto e adjacente, além da hipotenusa:
O nome disso é cateto oposto sobre a hipotenusa.
Chama-se cateto adjacente sobre a hipotenusa.
Deve-se ler cateto oposto sobre cateto adjacente.
Círculo Trigonométrico
O círculo trigonométrico é utilizado para se estudar as funções trigonométricas: seno, cosseno e tangente. Alguns estudiosos o chamam de círculo unitário.

Entenda a Geometria Euclidiana
No estudo da Matemática, a Geometria Euclidiana é a conhecida Geometria, só que em duas e três dimensões. Ela tem por base a chamada Teoria Euclidiana, que são postulados de Euclides de Alexandria.
Alguns conceitos de destaque na Geometria Euclidiana, quando se estuda a Trigonometria são: Lei dos Senos, dos Cossenos e das Tangentes.
A Lei dos Senos determina que, num dado triângulo, a razão entre o valor de um lado e o seno do seu ângulo oposto, sempre será constante.
Dessa maneira, para um triângulo ABC de lados a, b, c, aplica-se a Lei dos Senos pela fórmula seguinte:

Trigonometria: Lei dos Cossenos
A Lei dos Cossenos estipula que, em qualquer triângulo, o quadrado de um dos lados equivale à soma dos quadrados dos outros dois lados. Só que menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Dessa forma, sua fórmula é grafada da maneira seguinte:

Lei das Tangentes
A Lei das Tangentes institui a relação entre as tangentes de dois ângulos de um triângulo, com os comprimentos dos seus lados opostos.
Então, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, considera-se a expressão:

Trigonometria: o Teorema de Pitágoras
O Teorema de Pitágoras foi elaborado pelo grego Pitágoras de Samos, ao passo que é bastante usado nos estudos trigonométricos. Ele comprova que, no triângulo retângulo, composto por um ângulo interno de 90°, a soma dos quadrados de seus catetos é igual ao quadrado da sua hipotenusa:
a2 = c2+ b2
Leia-se a = hipotenusa; c e b = catetos

Onde a Trigonometria é aplicada?
Há várias aplicações da Trigonometria, além das funções trigonométricas, sendo muitos os exemplos. A técnica da triangulação é utilizada na Astronomia visando criar uma estimativa da distância das estrelas próximas.
Em Geografia, a triangulação é usada para estimar quais as distâncias entre divisas, inclusive em sistemas de navegação por satélite. Já as funções seno e cosseno são essenciais para a Teoria das Funções Periódicas, que descrevem as ondas luminosas e sonoras.
Só que a Trigonometrias é usada ainda em teoria musical, eletrônica, biologia, arquitetura, cartografia e engenharia. Ela é muito útil na navegação dos aviões e dos barcos. Na teoria dos números, atualmente sua utilização maior está na criptologia, posto se tratar de sistema que torna seguro operar transações bancárias e se comunicar pela internet.
Leia também sobre a porcentagem, o que é, como calculá-la e aplicações práticas.
Fonte: khan Academy, Matemática Básica, Wikipédia, Toda Matéria, Stoodi, Escola Kids, Brasil Escola, Alunos Online, Educa Mais Brasil, Guia dos Estudante.
Fonte das imagens: Khan Academy, Matemática Básica, Passeia Direto, Youtube, Descomplica, Wikipédia.