O cosseno é uma das razões trigonométricas, juntamente com o seno e a tangente. Eles servem para relacionar as medidas dos lados de um triângulo retângulo com as medidas dos seus ângulos.
Trigonometria é a área da matemática que estuda os lados e os ângulos dos triângulos, o que envolve o seno, cosseno e tangente.
O estudo das relações trigonométricas, ainda na antiguidade, foi muito importante para o desenvolvimento de muitas outras áreas importantes do conhecimento, que utilizam a matemática. Isso porque a maioria dos cálculos de distância usam a trigonometria.
O que é cosseno?
O cosseno é uma das razões trigonométricas, juntamente com o seno e a tangente. Sendo assim, o cosseno é uma função periódica limitada que é o resultado da razão entre o cateto adjacente e a hipotenusa. Desse modo, define-se a razão entre os lados do triângulo com a seguinte fórmula:

Dentro da trigonometria existem alguns ângulos que são chamados de notáveis, uma vez que o seu valor é calculado facilmente. Desse modo, temos os seguintes ângulos notáveis do cosseno:

Por fim, temos a lei dos cossenos, que é útil em questões trigonométricas que não envolvem um triângulo retângulo, ou seja, que não possui um ângulo reto. Nesse caso, essa lei é usada para solucionar problemas de um triângulo qualquer. Assim, temos as seguintes expressões matemáticas da lei dos cossenos:
-
a² = b² + c² – 2ab . CoA
-
b² = a + c² – 2ac . CosB
-
c² = a + b² – 2ac . CosC
Para que serve o cosseno?
O seno, cosseno e tangente servem para relacionar as medidas dos lados de um triângulo retângulo com as medidas dos seus ângulos. Sendo assim, elas são as relações trigonométricas ou razões trigonométricas.
Portanto, como essas relações são definidas a partir de um triângulo retângulo, vale a pena conhecer os elementos dessa figura. Primeiramente, o triângulo é um polígono de três lado, sendo que quando um dos ângulos é igual a 90º, ele recebe o nome de retângulo. Observe a imagem abaixo:
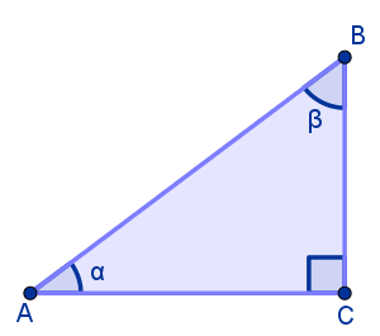
Na imagem, o ângulo reto está no vértice C do triângulo, sendo assim, os lados que partem desse vértice são chamados de adjacentes ao ângulo reto e são conhecidos como catetos. Por fim, o lado que sobra sempre é o maior do triângulo retângulo e é chamado de hipotenusa.
Para estabelecer o seno, cosseno e tangente, é preciso escolher um ângulo de referência. Por exemplo, vamos considerar o ângulo α. Neste caso, o cateto BC é o cateto oposto, e o lado AC é o cateto adjacente, pois BC é o lado oposto ao ângulo α.
Função cosseno
Define-se a função do cosseno da seguinte forma: f(x)=cos(x). Observe o exemplo a seguir:

Sendo assim, na função temos que o cosseno de um ângulo sempre estará sob o eixo das abscissas (x). Além disso, ele é positivo no 1º e 4º quadrantes, portanto, no 2º e 3º quadrantes os valores são negativos.
Domínio da função cosseno diz respeito ao conjunto dos números reais, logo, a imagem corresponde ao intervalo real [-1,1] ou -1 = cos x = 1. Por fim, o período é o mesmo que a função do seno:

Gráfico
Cossenoide é o nome dado ao gráfico da função cosseno, observe a sua representação abaixo:

Fontes: InfoEscola, Mundo educação, Educa Mais Brasil, SBM



