Os números binários são um sistema numérico com base em apenas dois algarismos: 0 e 1. Dessa forma, um número binário nada mais é do que uma representação alternativa de outro número.
O sistema binário possibilita a existência dos dispositivos com circuitos integrados (chips). Sendo assim, os números binários são usados nos computadores para representar números, caracteres, realizar operações lógicas e aritméticas.
Enfim, como o sistema binário usa apenas o 0 e 1, ele se difere do números decimais são os números formados a partir da combinação dos números: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Mas é possível fazer a conversão de binário para decimal e vice-versa.
O que são os números binários e para que servem?
O sistema binário é um sistema de numeração onde todas as quantidades são apresentadas com base em dois números: 0 e 1.
O sistema binário serve como base para a Álgebra Booliana, do matemático inglês George Boole. Com isso, é possível realizar operações lógicas e aritméticas usando apenas dois dígitos ou dois estados, tais como, sim ou não, verdadeiro ou falso, ligado ou desligado.
Inclusive, a eletrônica digital e computação têm como base o sistema binário e a lógica de Boole, que possibilita representar por circuitos eletrônicos digitais (portas lógicas) os números, caracteres, realizar operações lógicas e aritméticas.
Sendo assim, os programas de computadores são codificados de forma binária e armazenados nas mídias (memórias, discos e afins) com esse formato. Por exemplo, as informações que constam na memória RAM do computador, o formato é de voltagem mais alta (1) ou mais baixa (0).
Como funciona esse sistema de numeração?
O sistema binário funciona como um sistema de numeração posicional onde números só podem ser 0 ou 1, por exemplo: 1010011010. No dia a dia, o comum é usarmos os números decimais, que são formados por: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
No entanto, dentro de um computador, os números são sempre binários. Esses números são armazenados dentro do computador em grupos, normalmente de 8 bits.
Vale destacar que qualquer dispositivo que tenha circuitos integrados (chips), é possível apenas por causa do sistema binário. Além disso, como este sistema numérico é mais simples, já que usa apenas dois dígitos, é possível fazer o armazenamento dos números em forma física como campos magnéticos em um disco rígido, por exemplo.
Por causa dessa possibilidade da forma física dos números binários, é possível que eles existam dentro de um microprocessador, de uma memória ou de um disco rígido do computador ou ainda que viaje pela internet ou por uma rede wi-fi.
Leia também: História dos números – Contagem, evolução do homem e matemática
Como transformar um número decimal em número binário?
Os números decimais são os números formados a partir da combinação dos números: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. As mais diferentes combinações podem ser feitas com esses números, representando quantidades diferentes como, por exemplo: 150, 300 e 900.
Para transformar um número decimal em binário, é preciso fazer sucessivas divisões sobre a base, que é 2, até que não seja mais possível dividir.
Para calcular é simples. Pegamos um número de base 10 (decimal) e decompomos por 2 até não ser possível mais dividir. Com os resultados formamos um novo número de base 2. Agrupamos o último resultado seguido dos restos das divisões anteriores, do último para o primeiro. Por exemplo:
14(base10) = 1110(base2)
14 / 2 = 7 resto 0
7 / 2 = 3 resto 1
3 / 2 = 1 resto 1
Como transformar um número binário em decimal?
Para transformar um número binário em decimal, é preciso pegar cada um dos seus dígitos e o multiplicar pela base, que é 2, elevado à potência correspondente de acordo com a sua posição e, em seguida, somar os resultados.
Ou seja, para converter damos valores ao número 1 de acordo com a sua posição e somamos tudo. As posições são sempre potências de 2 (20, 21, 22, 23,..). Por exemplo, o número 11111011100 em decimal é:
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 210 = 1024 | 29 = 512 | 28 = 256 | 27 = 128 | 26 = 64 | 25 = 32 | 24 = 16 | 23 = 8 | 22 = 4 | 21 = 2 | 20 = 1 |
1024+512+256+128+64+16+8+4 = 2012
Vale destacar que não somamos os números 1, 2 nem 32, pois eles tinham 0 em suas respectivas posições no número binário.
Como montar palavras a partir de números binários?
Tendo como base o livro Computer Science Unplugged, podemos entender como funciona a linguagem computacional. O Unplugged utilizou números binários de até 5 dígitos, podendo variar em ordem crescente, do seguinte modo: 00000, 00001, 00010, 00011, 00100… Até 11111. Cada sequência dessa se chama byte.
Para facilitar o estabelecimento da correspondência, são usadas tabelas de conversão, onde cada byte se converte em um carácter e vise versa. Existem várias tabelas, uma das mais conhecida é a ASCII. Um exemplo do seu uso na conversão é:
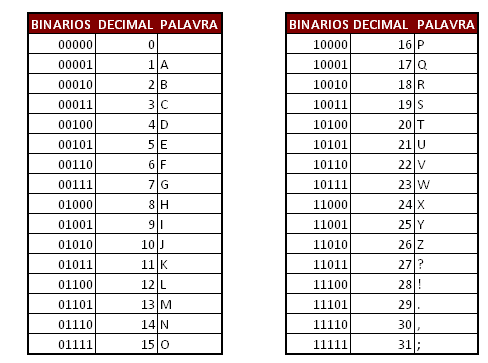
Enfim, essa tabela é apenas um exemplo, mas existem outras tabelas com base em qualquer sequência ou com outros caracteres, tais como letras minúsculas, letras acentuadas, símbolos etc.
E aí, gostou de aprender sobre os números binários? Então não deixe de conferir também: Número composto: O que é, Definição, fatoração e exemplos
Fontes: Canal Tech, Material public, Brasil Escola, Pronatec e, por fim, GCFGlobal.
Bibliografia:
- SILVA, Marcos Noé Pedro da. “Sistema de Numeração Binária”; Brasil Escola.
- GCFGLOBAL. Os números binários 2016.
- MENDES, Herman do Lago. Os Números Binários; do saber escolar ao saber científico. Jornal Internacional de Estudos em Educação Matemática [S.L.], v 10, n 1, p. 41; 13 set. 2017. Editora e Distribuidora Educacional.
- FREDERICO, Ana Carolina Vargas; Costa, Christine Sertã Números binários; uma proposta de ensino para a educação básica Rio de Janeiro 2020 65 p Dissertação de Mestrado, Departamento de Matemática, PUC do Rio de Janeiro.



