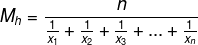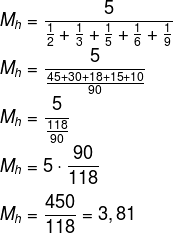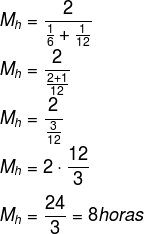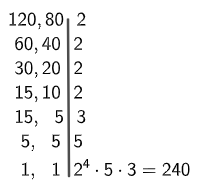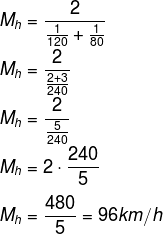A média harmônica é um tipo de média que costuma ser usada em situações onde se deseja a média entre duas ou mais taxas.
Sendo que a média harmônica geralmente é usada em situações que envolvem grandezas inversamente proporcionais.
Por exemplo, ela é útil no cálculo de tempo necessário para encher um recipiente levando em conta a vazão de uma torneira. Isso porque, vazão e tempo são grandezas inversamente proporcionais.
Quando usar a média harmônica?
A média harmônica deve ser usada quando a intenção é encontrar o valor que representa um conjunto. Sendo assim, ela é muito útil na estatística, por exemplo.
No entanto, ela não é a única opção disponível para representar um valor central.
Isso porque, existe também a média aritmética ponderada, a média aritmética simples, a média geométrica, a mediana e a moda.
Desse modo, o que vai determinar quais dessas serão usadas, é a situação. Ou seja, não existe uma medida central universalmente mais precisa para representar o valor central de um conjunto.
Ao invés disso, é preciso levar em conta a situação apresentada, para escolher a que melhor se encaixa.
De maneira geral, a média harmônica é escolhida em situações que envolvem grandezas inversamente proporcionais.
Fórmula
O cálculo da média ocorre pela divisão de n pela soma dos inversos dos elementos. Portanto, a fórmula é:
Sendo que:
-
Mh é a média harmônica
-
n é a quantidade de elementos
Como se calcula a média harmônica?
Para calcular a média harmônica de um conjunto de dados, é preciso lembrar o que é o inverso de um número. Dessa forma, seja x um número qualquer, o inverso de x é representado por:
Um detalhe importante é que se o número for uma fração, para encontrar o inverso dele, basta inverter o numerador com o denominador.
Para você entender melhor como fazer o cálculo da média harmônica, vamos a um exemplo. Vamos supor que temos um conjunto A (2, 3, 5, 6, 9), que tem cinco elementos.
Logo, o cálculo da média harmônica de A ocorre por:
Já para realizar a soma de frações, é preciso encontrar o mínimo múltiplo comum entre os denominadores:
O m.m.c (2, 3, 5, 6, 9) é igual a 90, sendo assim, é possível fazer a soma das frações no denominador:
Aplicações no dia a dia
No geral, a média harmônica é útil em qualquer conjunto numérico de dados. No entanto, existem algumas situações específicas em que ela é a melhor opção.
Vamos analisar isso em dois exemplos:
1- Vazão de torneiras
Vamos imaginar que para encher um tanque, uma torneira demore 12 horas. Contudo, para encher esse mesmo tanque, outra torneira leva 6 horas.
Desse modo, temos que descobrir quanto tempo demora para encher o tanque se as duas torneiras forem abertas ao mesmo tempo.
Primeiramente, é preciso observar que vazão e tempo são grandezas inversamente proporcionais. Isso porque, quanto maior a vazão da torneira, menor será o tempo que ela levará para encher o tanque.
Sendo assim, a média harmônica é útil para encontrar o tempo das duas torneiras. Portanto, temos que:
No caso, o 8 horas é o tempo, em média, de cada uma das duas torneiras. No entanto, elas serão ligadas juntas em um único tanque. Logo, é preciso dividir esse tempo por 2.
8 ÷ 2 = 4 horas
No fim das contas, leva 4 horas para encher o tanque com as duas torneiras.
2- Aplicação no cálculo de velocidade média
Vamos supor que um carro faça um percurso duas vezes. Na ida, ele faz o percurso com uma velocidade v1 = 80 km/h. Por outro lado, na volta, ele faz o mesmo percurso com velocidade de v2 = 120 km/h.
Portanto, temos que descobrir qual foi a velocidade média ao juntar-se ida e volta.
Neste caso, a média harmônica é usada, pois a distância é a mesma, de ida e de volta, mas a velocidade muda, logo, o tempo muda.
Ou seja, com o aumento da velocidade, o tempo para percorrer a mesma distância é menor. Dessa forma, as grandezas são inversamente proporcionais. Portanto, temos:
Calculando o m.m.c (120, 80):
Enfim temos que:
Fontes: Mundo educação e Brasil escola.